Zmień język :
drylin® T - konstrukcja systemu, pozioma, 1 szyna i 2 wózki lub 2 szyny i 4 wózki
Krok 2:
Sprawdzić, czy odległości między przyłożonymi siłami mieszczą się w dopuszczalnych wartościach (patrz maksymalne dopuszczalne odległości).
| Wariant: 1 szyna, 2 wózki | Wariant: 2 szyny, 4 wagony | |
|---|---|---|
| sy + sz | < | 2 wx - Y0 |
| ay + az | < | 2 wx - Y0 |
Krok 3:
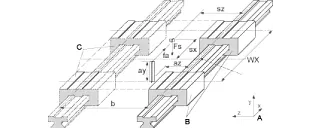
A = początek współrzędnych
B = stały namiar
C = namiar swobodny
Obliczanie wymaganej siły napędowej
Zmienne w obliczeniach
| Fa: | siła napędowa | [N] |
| Fs: | Siła masy | [N] |
| Fy, Fz: | Obciążenie łożyska w kierunku y lub z | [N] |
| sx, sy, sz: | Odległość siły bezwładności w kierunku x, y lub z | [mm] |
| ay, az: | Odległość siły napędowej w kierunku y lub z | [mm] |
| wx: | Odległość między wagonami na szynie | [mm] |
| LX: | Stała zależna od rozmiaru | [mm] |
| Zm: | Stała zależna od rozmiaru | [mm] |
| Y0: | Stała zależna od rozmiaru | [mm] |
| b: | Odległość między prowadnicami | [mm] |
| µ: | współczynnik tarcia, µ = 0 dla obciążeń statycznych, µ = 0,2 dla obciążeń dynamicznych | |
| ZW: | Liczba prowadnic na szynę |
Krok 4:
Obliczenie maksymalnego obciążenia łożyska
Stałe wartości
| Numer zamówienia | LX [mm] | ZM [mm] | Y0 [mm] |
|---|---|---|---|
| TW-01-15 | 29 | 16 | 11,5 |
| TW-01-20 | 35 | 23 | 15,0 |
| TW-01-25 | 41 | 25 | 19,0 |
| TW-01-30 | 49 | 29 | 21,5 |
Współczynniki
| 1 szyna, 2 wagony | 2 szyny, 3-4 wagony | |
|---|---|---|
| K1 | |(ay+Y0)/Wx| | |(ay+Y0)/Wx| |
| K2 | (sy+Y0)/Wx | (sy+Y0)/Wx |
| K3 | |az/Wx| | |az/Wx| |
| K4 | |sx/Wx| | |sx/Wx| |
| K5 | |sz/Wx| | |sz/Wx| |
| K6 | |(sy+Y0)/Zm| | |(sy+Y0)/b| |
| K7 | |sz/Zm| | |(sz/b)-0.5| |
Krok 5:
Sprawdzić maksymalne obciążenie najbardziej obciążonego łożyska z obciążeniem obliczonym w kroku nr 4.
Maksymalne dopuszczalne obciążenie
| Numer zamówienia | Fymax, Fzmax [N] |
|---|---|
| TW-01-15 | 2.000 |
| TW-01-20 | 3700 |
| TW-01-25 | 5.000 |
| TW-01-30 | 7.000 |
Krok 6:
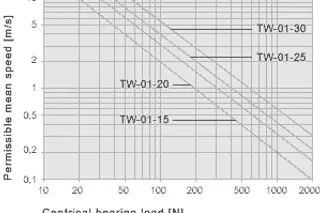
aby określić maksymalną dopuszczalną prędkość dla określonego obciążenia łożyska.
X = centralne obciążenie łożyska [N]
Y = dopuszczalna średnia prędkość [m/s]
Określenie maksymalnej dopuszczalnej prędkości dla obciążenia z kroku nr 4
Konsultacje
Z przyjemnością osobiście odpowiem na Państwa pytania

Konsultacje i dostawa
Osobista:
Od poniedziałku do piątku: 7:00–20:00
Sobota: 8:00–12:00
Online:
Umów spotkanie z ekspertem





